Dijkstra - A Visualization
- Aug 18, 2020
- 3 min read
Updated: Aug 27, 2020
The first algorithm that blew my mind was Dijkstra's shortest path algorithm. I originally came upon the algorithm while producing my 2D Top-Down Zombie Shooter, which you can read more about here. I was looking for a way to automate my zombies' movement and came upon a plugin that utilized the A* pathfinding algorithm used to move objects in the game-world. Upon seeing how the algorithm dynamically found the shortest path between the zombie and the player, I knew I had to know more about how it worked. After a few quick Google searches, I discovered that the A* pathfinding algorithm was a composite algorithm consisting of a Greedy-First graph traversal algorithm and Dijkstra's. I read up on a few implementations of the A* pathfinding algorithm and figured out that the real genius behind it was in Dijkstra's, though implementing a Greedy-First heuristic to improve average runtime for a given end-point from a single source is also a real stroke of genius. I then sought to implement my own version of Dijkstra's for my game, though my understanding of graph theory couldn't provide a solid solution, and eventually reverted back to the plugin that introduced me to the concept. However, I remained fascinated by Dijkstra's, and since enrolling in Northeastern University's Masters of Science in Computer Science program, I have only become more fond of the algorithm and graph theory in general.
Between the Spring and Summer semester of 2020, I used Unity to create a visualization of Dijkstra's pathfinding algorithm within a predetermined grid. The instance is unique in that all edges are weighted the same, and thus the shortest path primarily serves to maneuver around missing segments, similar to an enemy skirting the edges of object in a video game to reach the player.

When the graph is initially run, it produces an empty grid. Dijkstra's can be run on this grid, but it won't produce any real results, since it is technically a forest with N many components for N many nodes. The user must click the "Generate Graph" button to randomly generate connections between nodes.
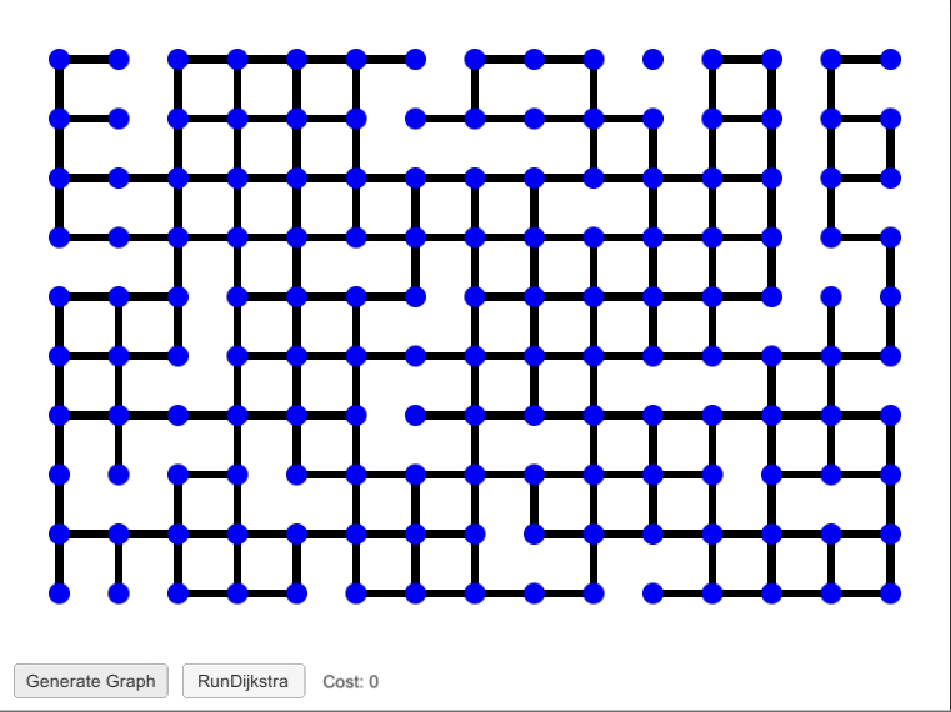
The graph can be generated as many times as the user wants. Each time "Generate Graph" is clicked, a new set of connections between nodes is set. There is no guarantee that the graph will result in a single connected components -- there may be multiple connected components that cannot be found from the source node, in which case, the cost will be listed as "infinity". Now that the graph is set, the user can click "Run Dijkstra", which randomly selects a start and an end node and uses Dijkstra's algorithm to find the shortest path between the two nodes.
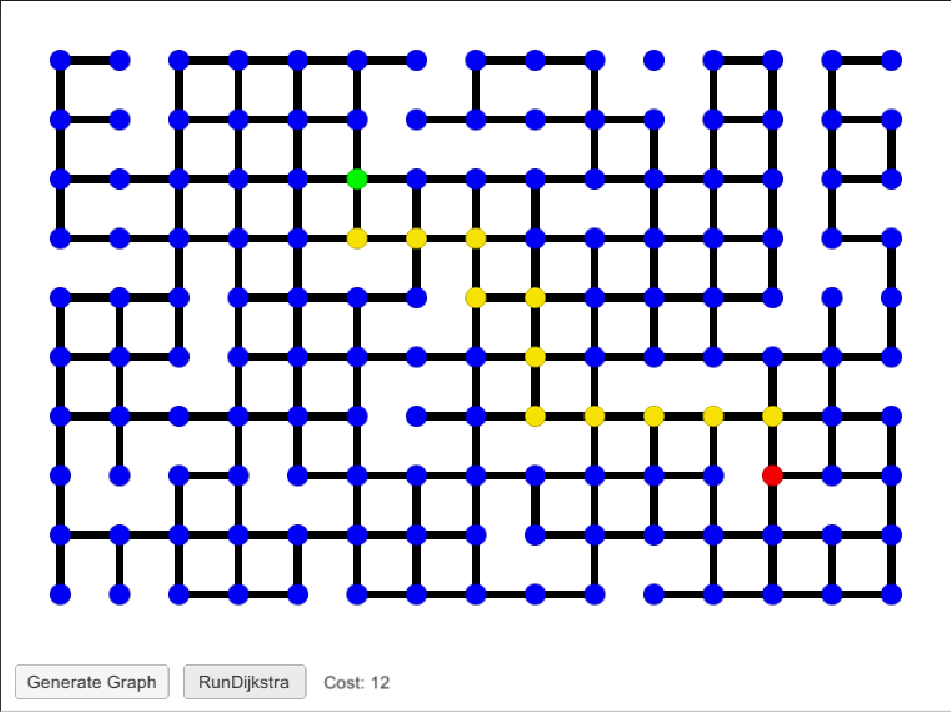
Once Dijkstra's has run, the start node of the search is colored in green, the end node is colored in red, and all nodes on the path from the start node to the end node are colored in yellow. Next to the "Run Dijkstra" button, there is a text field called "Cost", which shows the number of edges traversed in the shortest path to the end node from the start node. By clicking "Run Dijkstra" again on the same graph, the previous path with be cleared, and the process will be repeated on the same graph.
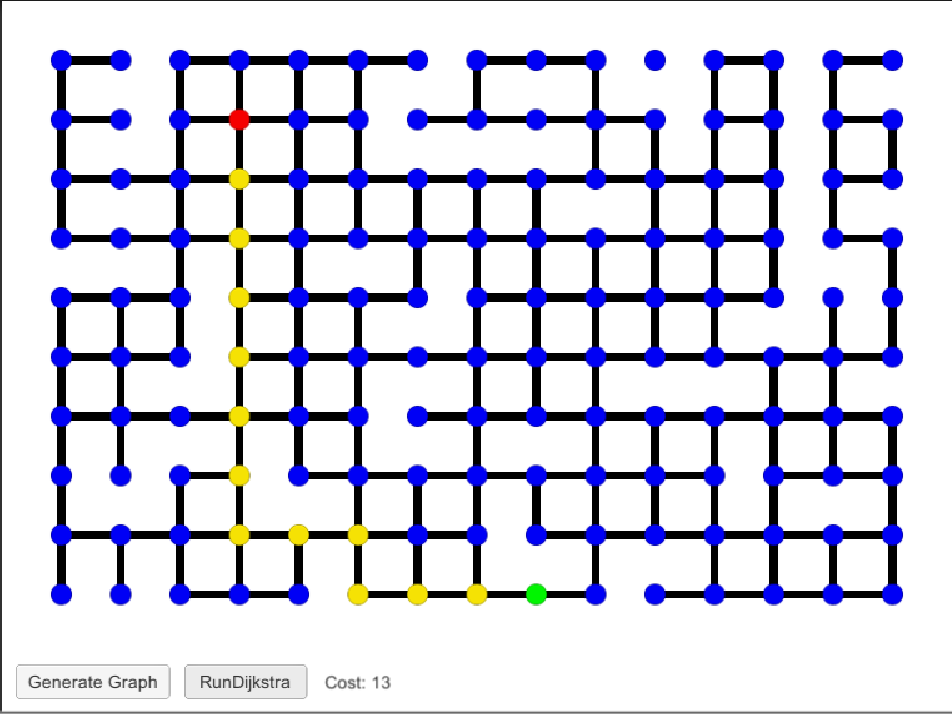
Should the user want to perform the search on a new graph, all they have to do is click "Generate Graph" and it will create a new blank graph.
My repository for this project can be found by following this link:



Comments